标签:树形DP
题目
题目描述
W 国的交通呈一棵树的形状。W 国一共有\(n - 1\)个城市和\(n\)个乡村,其中城市从\(1\)到\(n - 1\) 编号,乡村从\(1\)到\(n\)编号,且\(1\)号城市是首都。道路都是单向的,本题中我们只考虑从乡村通往首都的道路网络。对于每一个城市,恰有一条公路和一条铁路通向这座城市。对于城市i, 通向该城市的道路(公路或铁路)的起点,要么是一个乡村,要么是一个编号比\(i\)大的城市。 没有道路通向任何乡村。除了首都以外,从任何城市或乡村出发只有一条道路;首都没有往 外的道路。从任何乡村出发,沿着唯一往外的道路走,总可以到达首都。
W 国的国王小 W 获得了一笔资金,他决定用这笔资金来改善交通。由于资金有限,小 W 只能翻修\(n - 1\)条道路。小 W 决定对每个城市翻修恰好一条通向它的道路,即从公路和铁 路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利,于是根据人口调 查的数据,小 W 对每个乡村制定了三个参数,编号为\(i\)的乡村的三个参数是\(a_i\),\(b_i\)和\(c_i\)。假设 从编号为\(i\)的乡村走到首都一共需要经过\(x\)条未翻修的公路与\(y\)条未翻修的铁路,那么该乡村 的不便利值为
\[c_i \cdot (a_i + x) \cdot (b_i + y)\]在给定的翻修方案下,每个乡村的不便利值相加的和为该翻修方案的不便利值。 翻修\(n - 1\)条道路有很多方案,其中不便利值最小的方案称为最优翻修方案,小 W 自然 希望找到最优翻修方案,请你帮助他求出这个最优翻修方案的不便利值。
输入输出格式
输入格式
第一行为正整数\(n\)。
接下来\(n - 1\)行,每行描述一个城市。其中第\(i\)行包含两个数\(s_i,t_i\)。\(s_i\)表示通向第\(i\)座城市 的公路的起点,\(t_i\)表示通向第i座城市的铁路的起点。如果\(s_i > 0\),那么存在一条从第\(s_i\)座城 市通往第\(i\)座城市的公路,否则存在一条从第\(-s_i\)个乡村通往第i座城市的公路;\(t_i\)类似地,如 果\(t_i > 0\),那么存在一条从第\(t_i\)座城市通往第i座城市的铁路,否则存在一条从第\(-t_i\)个乡村通 往第\(i\)座城市的铁路。
接下来\(n\)行,每行描述一个乡村。其中第i行包含三个数\(a_i,b_i,c_i\),其意义如题面所示。
输出格式
输出一行一个整数,表示最优翻修方案的不便利值。
输入输出样例
输入样例#1
6
2 3
4 5
-1 -2
-3 -4
-5 -6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
输出样例#1
54
输入样例#2
9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
输出样例#2
548
输入样例#3
12
2 4
5 3
-7 10
11 9
-1 6
8 7
-6 -10
-9 -4
-12 -5
-2 -3
-8 -11
53 26 491
24 58 190
17 37 356
15 51 997
30 19 398
3 45 27
52 55 838
16 18 931
58 24 212
43 25 198
54 15 172
34 5 524
输出样例#3
5744902
说明
【样例解释 1】
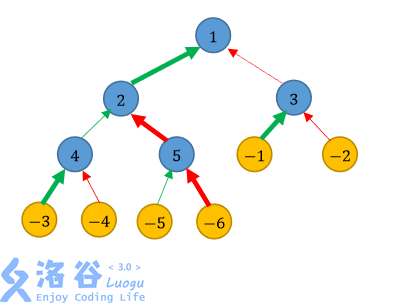
如图所示,我们分别用蓝色、黄色节点表示城市、乡村;用绿色、红色箭头分别表示 公路、铁路;用加粗箭头表示翻修的道路。
一种不便利值等于54的方法是:翻修通往城市2和城市5的铁路,以及通往其他城市的 公路。用→和⇒表示公路和铁路,用∗→和∗⇒表示翻修的公路和铁路,那么:
编号为1的乡村到达首都的路线为:-1 ∗→ 3 ⇒ 1,经过0条未翻修公路和1条未翻修铁 路,代价为3 × (1 + 0) × (2 + 1) = 9;
编号为2的乡村到达首都的路线为:-2 ⇒ 3 ⇒ 1,经过0条未翻修公路和2条未翻修铁 路,代价为2 × (1 + 0) × (3 + 2) = 10;
编号为3的乡村到达首都的路线为:-3 ∗→ 4 → 2 ∗→ 1,经过1条未翻修公路和0条未 翻修铁路,代价为3 × (2 + 1) × (1 + 0) = 9;
编号为4的乡村到达首都的路线为:-4 ⇒ 4 → 2 ∗→ 1,经过1条未翻修公路和1条未翻 修铁路,代价为1 × (2 + 1) × (3 + 1) = 12;
编号为5的乡村到达首都的路线为:-5 → 5 ∗⇒ 2 ∗→ 1,经过1条未翻修公路和0条未 翻修铁路,代价为2 × (3 + 1) × (1 + 0) = 8;
编号为6的乡村到达首都的路线为:-6 ∗⇒ 5 ∗⇒ 2 ∗→ 1,经过0条未翻修公路和0条未翻修铁路,代价为1 × (3 + 0) × (2 + 0) = 6;
总的不便利值为9 + 10 + 9 + 12 + 8 + 6 = 54。可以证明这是本数据的最优解。
【样例解释 2】
在这个样例中,显然应该翻修所有公路。
【数据范围】
一共20组数据,编号为1 ∼ 20。
对于编号\(\le 4\)的数据,\(n \le 20\);
对于编号为5 ∼ 8的数据,\(a_i,b_i,c_i \le 5\),\(n \le 50\);
对于编号为9 ∼ 12的数据,\(n \le 2000\);
对于所有的数据,\(n \le 20000\),\(1 \le a_i,b_i \le 60\),\(1 \le c_i \le 10^9\),\(s_i,t_i\)是\([-n,-1] \cup (i,n - 1]\)内的整数,任意乡村可以通过不超过40条道路到达首都。
题解
在考场上只会20分暴力,自闭了qwq
直接考虑树形DP
设\(f[u][i][j]\)为从根节点到u节点经过了i条没经过标记的L边和j条没经过标记的R边
- 对于每个叶子节点直接枚举最佳答案\(f[u][j][j]=c_u(a_u+i)(b_u+j)\)
- 对于每个非叶子节点枚举左右删去哪条边\(f[u][i][j]=min\{ f[lson][i+1][j]+f[rson][i][j],f[lson][i][j]+f[rson][i][j+1]\}\)
code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dep(i,a,b) for(int i=a;i>=b;i--)
#define ll long long
#define mem(x,num) memset(x,num,sizeof x)
#define reg(x) for(int i=last[x];i;i=e[i].next)
using namespace std;
inline ll read(){
ll f=1,x=0;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
//******head by yjjr******
#define lson Num[s[u]]
#define rson Num[t[u]]
const int maxn=5e4+6;
int n,m,Top,Tot,a[maxn],b[maxn],c[maxn],s[maxn],t[maxn],Num[maxn],Sta[maxn];
ll f[106][106][106];
void dfs(int u,int x,int y){
int now=Num[u]=Top?Sta[Top--]:++Tot;
if(!s[u]){
rep(i,0,x)rep(j,0,y)f[now][i][j]=(ll)c[u]*(a[u]+i)*(b[u]+j);
return;
}
dfs(s[u],x+1,y);dfs(t[u],x,y+1);
rep(i,0,x)rep(j,0,y)f[now][i][j]=min(f[lson][i+1][j]+f[rson][i][j],f[lson][i][j]+f[rson][i][j+1]);
Sta[++Top]=lson,Sta[++Top]=rson;
}
int main(){
n=read();m=2*n-1;
rep(i,1,n-1){
int u=read(),v=read();
if(u<0)s[i]=n-u-1;else s[i]=u;
if(v<0)t[i]=n-v-1;else t[i]=v;
}
rep(i,n,m)a[i]=read(),b[i]=read(),c[i]=read();
dfs(1,0,0);
cout<<f[Num[1]][0][0]<<endl;
return 0;
}