标签:竞赛图,哈密顿回路,DP
题目
Description
给出一个n个点的有向图,任意两个点之间有且仅一条有向边。 对于每个点v,求出从v出发的一条经过点数最多,且没有重复经过同一个点两次及两次以上的简单路径。
Input
第一行包含一个正整数n(2<=n<=2000),表示点数。 接下来n-1行,其中的第i行有i-1个数 如果第j个数是1,那么表示有向边j->i+1,如果是0,那么表示有向边j<-i+1。
Output
输出n行,第i行首先包含一个正整数k,表示从i点出发的最优路径所经过的点数 接下来k个正整数,依次表示路径上的每个点。 若有多组最优解,输出任意一组。
Sample Input
4
1
1 1
1 0 1
Sample Output
4 1 2 3 4
3 2 3 4
3 3 4 2
3 4 2 3
分析
竞赛图就是n个点的有向图,任意两个点之间有且仅一条有向边
竞赛图一定存在哈密顿路径
然后强连通的竞赛图一定存在哈密顿回路
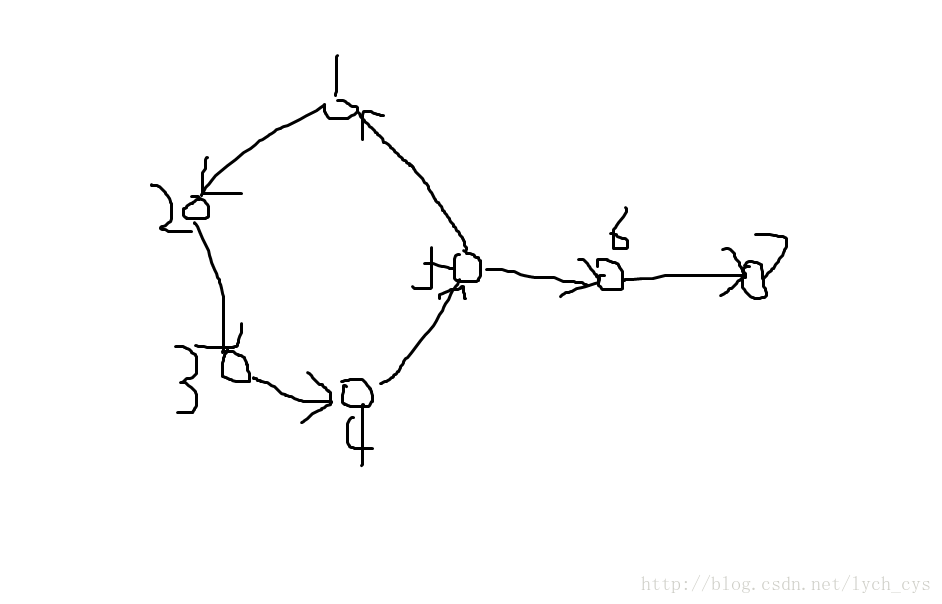
转一张lyc大爷的图qwq
-
存在一条6->1的路径,直接连上就好
-
存在一条x->6->nxt[x]的路径
-
6不指向环上任何一个点,这时候一定存在链上其他的点指向环上(因为这个图是强联通的)
这样我们就构造出了一个强联通竞赛图的哈密顿回路
把给出的竞赛图tarjan缩点,每个点是一个强联通分量,这就变成了DAG
每个强联通分量中找出一个哈密顿回路
那么发现不管从哪个点进入强联通分量都可以遍历这个环然后到达这个强联通分量指向的下一个强联通分量
然后DP计算长度即可
code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dep(i,a,b) for(int i=a;i>=b;i--)
#define ll long long
#define mem(x,num) memset(x,num,sizeof x)
#define reg(x) for(int i=last[x];i;i=e[i].next)
using namespace std;
inline ll read(){
ll f=1,x=0;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
//**********head by yjjr**********
const int maxn=2e3+6;
int n,dfn[maxn],low[maxn],scc[maxn],size[maxn],top,num,tim,st[maxn];
int nxt[maxn],h[maxn],m,nxtscc[maxn],f[maxn],nxtdp[maxn];
bool a[maxn][maxn],vis[maxn],can[maxn],b[maxn][maxn];
void pushin(int x){
vis[x]=1;
rep(i,1,m)if(a[h[i]][x])can[h[i]]=1;
}
void getnxt(){
int head=h[1],tail=h[1];
rep(i,2,m){
int x=h[i];
if(a[x][head]){nxt[x]=head;head=x;continue;}
for(int now=head,last=0;;last=now,now=nxt[now]){
if(last==tail){nxt[tail]=x;tail=x;break;}
if(a[x][now]){nxt[x]=now;nxt[last]=x;break;}
}
}
int end=head;pushin(head);
while(end^tail){
int x=nxt[end];
if(a[x][head]){end=x;pushin(x);continue;}
for(int now=head,last=0;;last=now,now=nxt[now]){
if(a[x][now]){nxt[last]=x;nxt[end]=head;end=x;head=now;pushin(x);break;}
if(last==end){
int newend,y;
rep(i,1,m)if(!vis[h[i]]&&can[h[i]]){newend=h[i];break;}
for(int i=head;;i=nxt[i])if(a[newend][i]||i==end){y=i;break;}
for(int i=nxt[end];;i=nxt[i]){pushin(i);if(i==newend)break;}
nxt[end]=head;head=y;end=newend;
for(int now=head;;now=nxt[now])if(nxt[now]==y){nxt[now]=x;break;}
break;
}
}
}
nxt[tail]=head;
rep(i,1,m)vis[h[i]]=can[h[i]]=0;
}
void dfs(int x){
int tmp=0;dfn[x]=low[x]=++tim;st[++top]=x;
rep(y,1,n)if(a[x][y])
if(!dfn[y])dfs(y),low[x]=min(low[x],low[y]);
else if(!scc[y])low[x]=min(low[x],dfn[y]);
if(dfn[x]==low[x]){
nxtscc[++num]=x;
m=0;
while(tmp^x)tmp=st[top--],size[scc[tmp]=num]++,h[++m]=tmp;
getnxt();
}
}
void solve(int x){
if(!x)return;
printf(" %d",x);for(int i=nxt[x];i^x;i=nxt[i])printf(" %d",i);
solve(nxtscc[nxtdp[scc[x]]]);
}
inline int getdp(int x){
if(f[x])return f[x];
rep(i,1,num)
if(b[x][i]&&x!=i){
int g=getdp(i);
if(f[x]<g)f[x]=g,nxtdp[x]=i;
}
f[x]+=size[x];
return f[x];
}
int main(){
n=read();
rep(j,2,n)rep(i,1,j-1)a[i][j]=read(),a[j][i]=a[i][j]^1;
rep(i,1,n)if(!dfn[i])dfs(i);
rep(i,1,n)rep(j,1,n)
if(a[i][j])b[scc[i]][scc[j]]|=1;
rep(i,1,num)getdp(i);
rep(i,1,n)
printf("%d",f[scc[i]]),solve(i),puts("");
return 0;
}