标签:状压DP
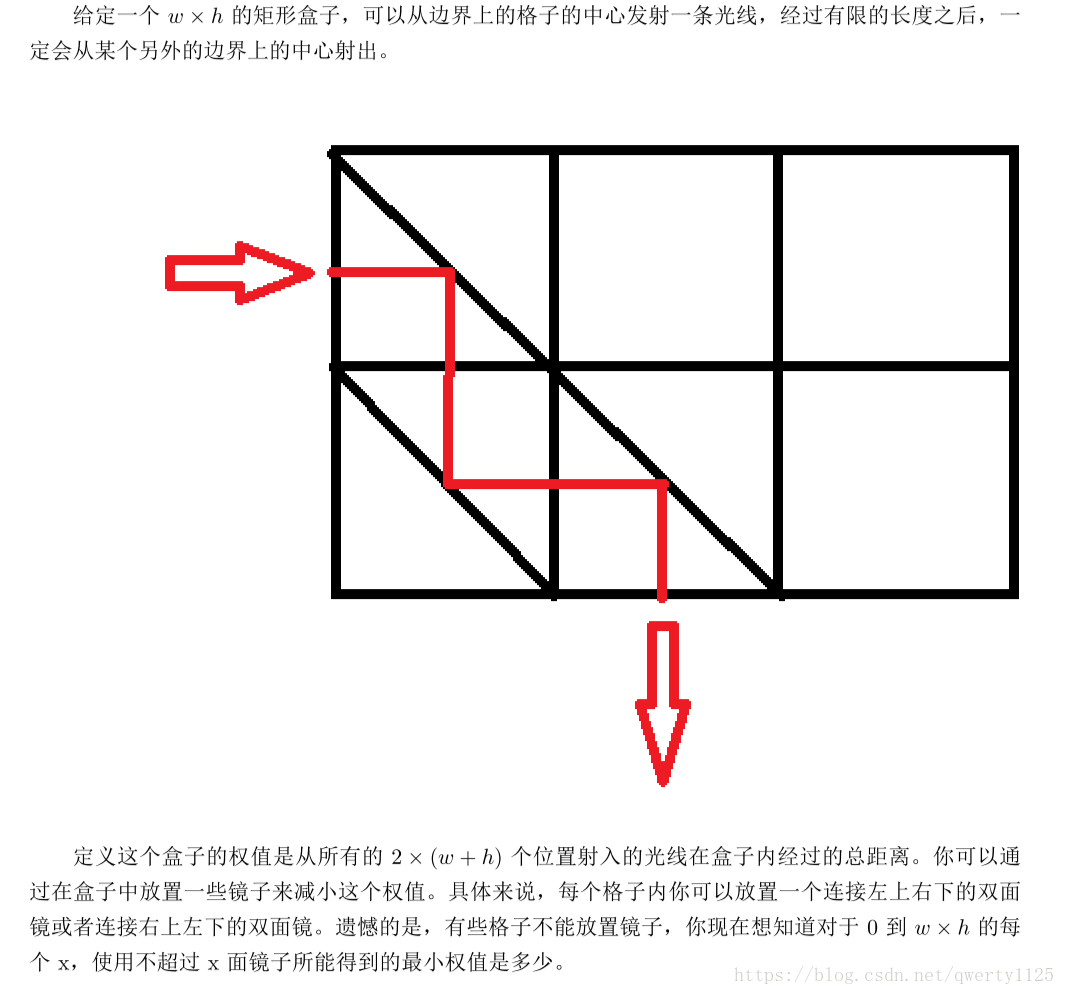
题目
分析
结论:当最优情况下,每行每列镜子的个数都为偶数
题目可以转化为摆放镜子,使得格子中产生的光环最长
所以不需要考虑镜子到底放什么方向
于是我们直接状压一列镜子当前的奇偶性进行转移
时间复杂度\(O(4^n*n*m^2)\)
code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dep(i,a,b) for(int i=a;i>=b;i--)
#define ll long long
#define mem(x,num) memset(x,num,sizeof x)
#define reg(x) for(int i=last[x];i;i=e[i].next)
using namespace std;
inline ll read(){
ll f=1,x=0;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
//**********head by yjjr**********
#define inf 1e9
const int maxn=(1<<10)+6;
char st[26][26];
int n,m,h[maxn],cnt[maxn],f[maxn][200],g[maxn][200],ans[maxn];
int main()
{
freopen("mirror.in","r",stdin);
freopen("mirror.out","w",stdout);
n=read(),m=read();
rep(i,1,n)scanf("%s",st[i]+1);
rep(sta,0,(1<<n)-1){
int t=0,x=-1;
rep(i,0,n-1)
if((sta>>i)&1){
t+=x*i;
x*=-1;
}
if(x==1)h[sta]=-inf;else h[sta]=t;
}
rep(sta,0,(1<<n)-1)cnt[sta]=cnt[sta>>1]+(sta&1);
rep(sta,0,(1<<n))rep(i,0,n*m)f[sta][i]=-inf;
f[0][0]=0;
rep(j,1,m){
memcpy(g,f,sizeof f);
rep(sta,0,(1<<n))rep(i,0,n*m)f[sta][i]=-inf;
int tmp=0;
rep(i,1,n)if(st[i][j]=='1')tmp^=1<<i-1;
rep(sta,0,(1<<n))
rep(i,0,n*m)
if(g[sta][i]>-inf){
for(int s=tmp;;s=(s-1)&tmp){
int t=g[sta][i]+h[s],nm=cnt[s],nm2=cnt[s&sta];
t+=j*(nm2+nm2-nm);
f[sta^s][i+nm]=max(f[sta^s][i+nm],t);
if(!s)break;
}
}
}
rep(i,0,n*m)ans[i]=f[0][i];
rep(i,1,n*m)ans[i]=max(ans[i],ans[i-1]);
rep(i,0,n*m)printf("%d ",4*n*m-2*ans[i]);printf("\n");
return 0;
}